Pragmatic Bookshelf Brain Teaser
Saw a challenge from the Pragmatic Bookshelf on Mastodon
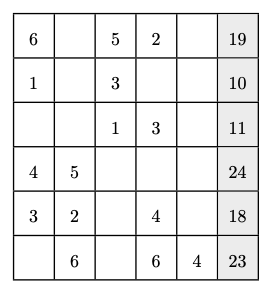
Fill each column with the digits 1 through 6 without repeating or omitting digits so the sums in the right column are the total of each row. A digit may appear more than one across rows.
Because putting that matrix into alt-text is weird, here’s a table!
| C1 | C2 | C3 | C4 | C5 | TOTAL |
|---|---|---|---|---|---|
| 6 | 5 | 2 | 19 | ||
| 1 | 3 | 10 | |||
| 1 | 3 | 11 | |||
| 4 | 5 | 24 | |||
| 3 | 2 | 4 | 18 | ||
| 6 | 5 | 4 | 23 |
Let’s Talk About It
This …
I suppose I have to say it.
This looks like a job for Recursion!
We’re placing a digit into a place in a matrix, proceeding, then testing at the end. We’re returning arrayrefs, and if we have the answer, it’ll be a full one. If not, [].
I expand my habitual use of List::Util, adding first and any to my bag of tricks. any is a boolean, checking an array for anything. Here, any { /x/ } @flatten tests if any of the elements in @flatten contain the letter x. Within my code, I’m using x as the placeholder for unfilled elements, so we can tell if the matrix has unfilled spots.
We then fill the spots in the array, and I use first to find the indexes we need to fill, with $row = first { 'x' eq $matrix->[$_][$col] } 1 .. 6.
We’re supposed to have each column use the numbers 1 through 6, so I use hashes and grep to discern the numbers in each column not already used, and then only use those numbers to fill in the column. Because of this, I don’t have to test if the column are correct, because they can’t not be. I test by sum, which is kinda halfhearted.
I feel I should mention that you don’t need to make a program to solve this. After being hung up a bit, I put the numbers into a spreadsheet, used a few =SUM() lines because I didn’t want to do simple addition if I could get the computer to do it, and was able to discern the numbers by hand, then use that as a test set to make sure my recursion was working.
Show Me The Code!
#!/usr/bin/env perl
use strict;
use warnings;
use experimental qw{ say signatures state fc };
use List::Util qw{ any first sum0 };
my $array = [
[qw{ 6 x 5 2 x }],
[qw{ 1 x 3 x x }],
[qw{ x x 1 3 x }],
[qw{ 4 5 x x x }],
[qw{ 3 2 x 4 x }],
[qw{ x 6 x 6 4 }],
];
my @totals = qw{19 10 11 24 18 23};
my $matrix = fill_matrix( $array, \@totals );
say 'OUTPUT';
say join "\n", map { join ' ', $_->@* } $matrix->@*;
exit;
sub fill_matrix ( $matrix, $totals, $col = 0 ) {
my @flat = map { $_->@* } $matrix->@*;
if ( any { $_ eq 'x' } @flat ) {
no warnings;
my @column = map { $_->[$col] } $matrix->@*;
if ( !any { /x/ } @column ) {
return fill_matrix( $matrix, $totals, $col + 1 );
}
my $row = first { 'x' eq $matrix->[$_][$col] } 1 .. 6;
my %list;
my @list = 1 .. 6;
$list{$_}++ for @column;
my @needed = grep { !$list{$_} } @list;
my $copy;
for my $i ( 0 .. -1 + scalar $matrix->@* ) {
my @row = $matrix->[$i]->@*;
push $copy->@*, \@row;
}
for my $n (@needed) {
$copy->[$row][$col] = $n;
my $return = fill_matrix( $copy, $totals, $col );
return $return if scalar $return->@*;
}
return [];
}
else {
for my $i ( 0 .. -1 + scalar $matrix->[0]->@* ) {
my @col = map { $matrix->[$_][$i] } 0 .. 5;
my $sum = sum0 @col;
return [] if $sum != 21;
}
for my $i ( 0 .. 5 ) {
my $t = $totals->[$i];
my $sum = sum0 $matrix->[$i]->@*;
if ( $sum ne $totals->[$i] ) {
return [];
}
}
return $matrix;
}
}
$ ./prag_array.pl
OUTPUT
6 1 5 2 5
1 3 3 1 2
2 4 1 3 1
4 5 4 5 6
3 2 6 4 3
5 6 2 6 4