Think Inside The Box: Weekly Challenge #152 Pt. 2
TASK #2 › Rectangle Area
Submitted by: Mohammad S Anwar
You are given coordinates bottom-left and top-right corner of two rectangles in a 2D plane.Write a script to find the total area covered by the two rectangles.
So, I spent a lot of time overthinking this one, coming up with a taxonomy of overlap that I might use to map this out, until I got to that duh moment.
I found a StackOverflow answer about overlapping rectangles and saw this:
return std::max(rectA.left, rectB.left) < std::min(rectA.right, rectB.right)
&& std::max(rectA.top, rectB.top) < std::min(rectA.bottom, rectB.bottom);
And that tab sat open, barly skimmed until I got it. You don’t need to find the parts of Rectangle A that stick out of Rectangle B. You simply need to find the Overlap.
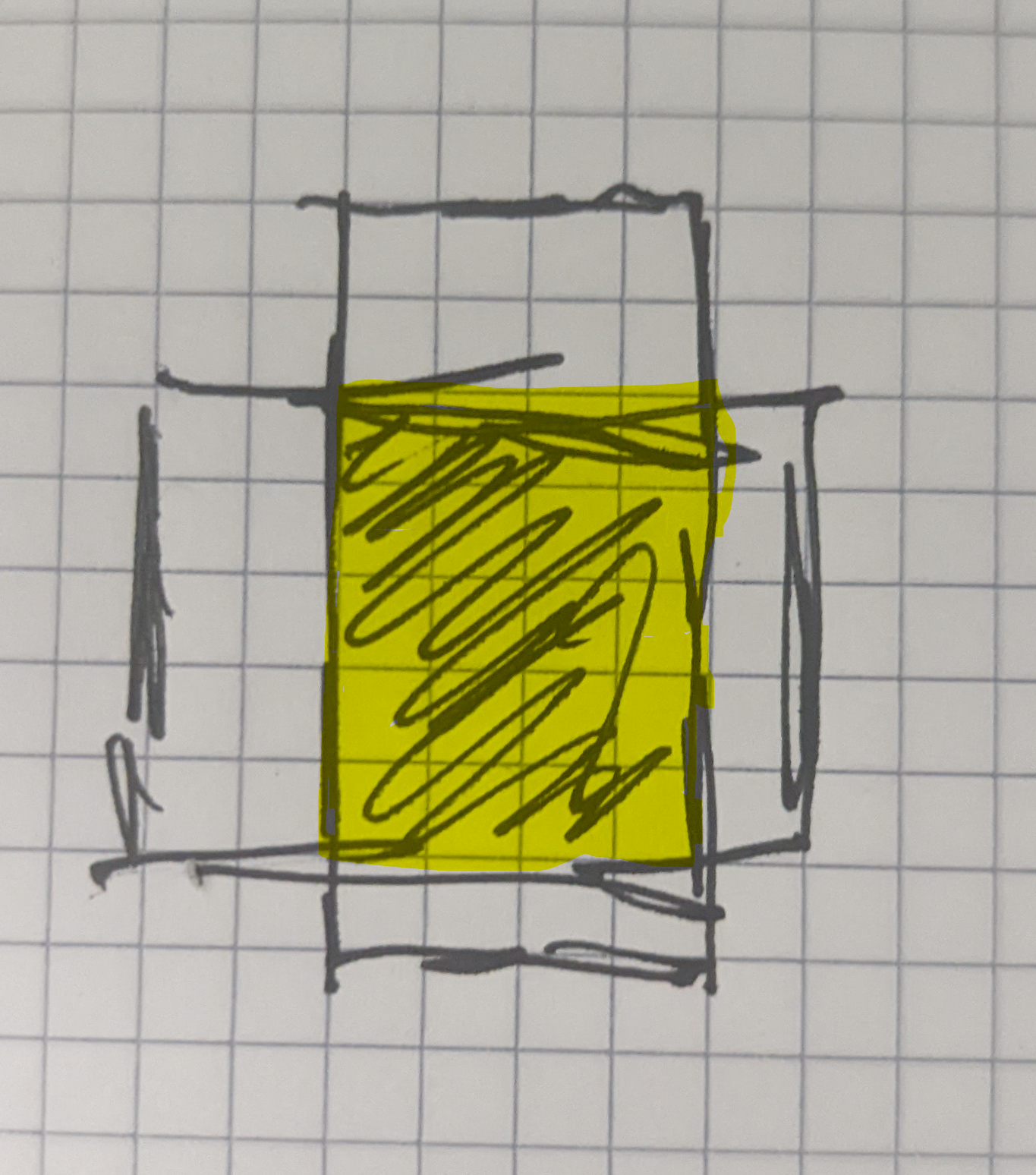
So, once you get that, then you know that the left and the bottom are defined as the max of the mins, and the top and right are defined by the min of the maxs.
I was expecting to do much more work and added code to map out the rectangles, meaning I created a lot of overhead before I got how easy this was. (I was even sure I should make Point, Line and Rectangle objects in Object::Pad) If this was real code, I’d re-engineer it so the make_rectangle function wasn never used or needed. Alas…
Show Me The Code!
#!/usr/bin/env perl
use strict;
use warnings;
use feature qw{ say postderef signatures state };
no warnings qw{ experimental };
use List::Util qw{ min max sum };
my @examples;
push @examples, [ [ [ -1, 0 ], [ 2, 2 ] ], [ [ 0, -1 ], [ 4, 4 ] ] ];
push @examples, [ [ [ -3, -1 ], [ 1, 3 ] ], [ [ -1, -3 ], [ 2, 2 ] ] ];
push @examples, [ [ [ 0, 0 ], [ 1, 1 ] ], [ [ 2, 2 ], [ 3, 3 ] ] ];
push @examples, [ [ [ 0, 0 ], [ 1, 1 ] ], [ [ 1, 1 ], [ 3, 3 ] ] ];
push @examples, [ [ [ 0, 1 ], [ 5, 2 ] ], [ [ 2, 0 ], [ 4, 4 ] ] ];
for my $e (@examples) {
my $area = find_area( $e->[0], $e->[1] );
say <<"END";
Input: Rectangle 1 => ($e->[0][0][0],$e->[0][0][1]), ($e->[0][1][0],$e->[0][1][1])
Rectangle 2 => ($e->[1][0][0],$e->[1][0][1]), ($e->[1][1][0],$e->[1][1][1])
Output: $area
END
}
sub find_area ( @r ) {
my @ro = map { make_rectangle($_) } @r;
my $overlap = has_overlap(@ro);
my $area = 0;
if ($overlap) {
my $overlap = find_overlap(@r);
$area = sum map { area($_) } @ro;
$area -= area($overlap);
}
else {
$area = sum map { area($_) } @ro;
}
return $area;
}
sub area ( $r ) {
my $minx = min map { $_->[0] } $r->@*;
my $maxx = max map { $_->[0] } $r->@*;
my $miny = min map { $_->[1] } $r->@*;
my $maxy = max map { $_->[1] } $r->@*;
my $x = $maxx - $minx;
my $y = $maxy - $miny;
return $x * $y;
}
sub find_overlap ( $r1, $r2 ) {
my $maxx1 = max map { $_->[0] } $r1->@*;
my $maxx2 = max map { $_->[0] } $r2->@*;
my $maxy1 = max map { $_->[1] } $r1->@*;
my $maxy2 = max map { $_->[1] } $r2->@*;
my $minx1 = min map { $_->[0] } $r1->@*;
my $minx2 = min map { $_->[0] } $r2->@*;
my $miny1 = min map { $_->[1] } $r1->@*;
my $miny2 = min map { $_->[1] } $r2->@*;
my $minx = max( $minx1, $minx2 );
my $miny = max( $miny1, $miny2 );
my $maxx = min( $maxx1, $maxx2 );
my $maxy = min( $maxy1, $maxy2 );
return [ [ $minx, $miny ], [ $maxx, $maxy ] ];
}
sub has_overlap ( $r1, $r2 ) {
my $maxx1 = max map { $_->[0] } $r1->@*;
my $maxx2 = max map { $_->[0] } $r2->@*;
my $maxy1 = max map { $_->[1] } $r1->@*;
my $maxy2 = max map { $_->[1] } $r2->@*;
my $minx1 = min map { $_->[0] } $r1->@*;
my $minx2 = min map { $_->[0] } $r2->@*;
my $miny1 = min map { $_->[1] } $r1->@*;
my $miny2 = min map { $_->[1] } $r2->@*;
return max( $minx1, $minx2 ) < min( $maxx1, $maxx2 )
&& max( $miny1, $miny2 ) < min( $maxy1, $maxy2 ) ? 1 : 0;
}
sub within ( $r1, $r2 ) {
my $within = 0;
my $minx = min map { $_->[0] } $r1->@*;
my $maxx = max map { $_->[0] } $r1->@*;
my $miny = min map { $_->[1] } $r1->@*;
my $maxy = max map { $_->[1] } $r1->@*;
for my $p ( $r2->@* ) {
my $x = $p->[0];
my $y = $p->[1];
if ( $x < $maxx
&& $x > $minx
&& $y < $maxy
&& $y > $miny )
{
$within++;
}
}
return $within;
}
sub make_rectangle ( $r ) {
my @points;
my @x = map { $_->[0] } $r->@*;
my @y = map { $_->[1] } $r->@*;
for my $x (@x) {
for my $y (@y) {
push @points, [ $x, $y ];
}
}
return \@points;
}
sub draw_rectangles( @r ) {
my @x = map { $_->[0] } map { $_->@* } @r;
my @y = map { $_->[1] } map { $_->@* } @r;
my $minx = min(@x);
my $maxx = max(@x);
my $miny = min(@y);
my $maxy = max(@y);
my @xr = $minx - 1 .. $maxx + 1;
my @yr = reverse $miny - 1 .. $maxy + 1;
my @r2;
for my $r (@r) {
my $rec;
my @x = map { $_->[0] } $r->@*;
my @y = map { $_->[1] } $r->@*;
for my $x (@x) {
for my $y (@y) { push $rec->@*, [ $x, $y ]; }
push @r2, $rec;
}
}
my @graph;
for my $y (@yr) {
my $row = [];
for my $x (@xr) {
my $s = ' ';
$s = '.' if $x == 0;
$s = '.' if $y == 0;
$s = '+' if $x == 0 && $y == 0;
my $pp = 0;
for my $r (@r2) {
$pp++;
for my $p ( $r->@* ) {
if ( $p->[0] == $x ) {
if ( $p->[1] == $y ) { $s = $pp; }
}
}
}
push $row->@*, $s;
}
push @graph, $row;
}
say join "\n", '', ( map { join ' ', $_->@* } @graph ), '';
}
$ ./ch-2.pl
Input: Rectangle 1 => (-1,0), (2,2)
Rectangle 2 => (0,-1), (4,4)
Output: 22
Input: Rectangle 1 => (-3,-1), (1,3)
Rectangle 2 => (-1,-3), (2,2)
Output: 25
Input: Rectangle 1 => (0,0), (1,1)
Rectangle 2 => (2,2), (3,3)
Output: 2
Input: Rectangle 1 => (0,0), (1,1)
Rectangle 2 => (1,1), (3,3)
Output: 5
Input: Rectangle 1 => (0,1), (5,2)
Rectangle 2 => (2,0), (4,4)
Output: 11