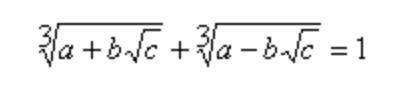It's Triplets!: Weekly Challenge #148
TASK #1 › Eban Numbers
Submitted by: Mohammad S Anwar Write a script to generate all Eban Numbers <= 100.
An Eban number is a number that has no letter ‘e’ in it when the number is spelled in English (American or British).
Here, we could either hack together something that knows the rules to spelling numbers, hoping you find all the corner cases.
Or
You could find something that already has done that.
Like Lingua::EN::Numbers. CPAN is truly a wonderful thing.
So, for the numbers between zero and 100, we convert to text and grep for e. Easy!
Show Me The Code!
#!/usr/bin/env perl
use strict;
use warnings;
use feature qw{ say postderef signatures state };
no warnings qw{ experimental };
use Lingua::EN::Numbers qw( num2en );
# You COULD try to make up a way to do this, but this wheel has been
# invented already and is sufficiently round.
my @numbers;
for my $i ( 0 .. 100 ) {
my $e = num2en $i;
next if $e =~ /e/mx;
push @numbers, $i;
}
say join ', ', @numbers;
2, 4, 6, 30, 32, 34, 36, 40, 42, 44, 46, 50, 52, 54, 56, 60, 62, 64, 66
TASK #2 › Cardano Triplets
Submitted by: Mohammad S Anwar Write a script to generate first 5 Cardano Triplets.
A triplet of positive integers (a,b,c) is called a Cardano Triplet if it satisfies the below condition.
This is, or can be, fairly straitforward. Go through a lot of numbers and test them. Once I have three numbers, I use Algorithm::Permuteto put together all possible permutations.
I’ll point out a thing that I was having problems with. Once I got cube roots worked out (Thank you, Perlmonks!), I put it into a function, then found that cuberoot( $a - $b * $sqrtc) would return NaN, meaning Perl didn’t think it was a number.
I searched and found a Khan Academy video, which pointed out that the cube root of a negative number is equal to the cube root of that number as a positive times the cube root of -1, which is -1. So, take the absolute value of the second part, take the cube root, then multiply by -1.
Show Me The Code!
#!/usr/bin/env perl
use strict;
use warnings;
use feature qw{ say postderef signatures state };
no warnings qw{ experimental };
use Algorithm::Permute;
my @triplets;
my $i = 0;
while ( scalar @triplets < 5 ) {
for my $j ( 1 .. $i ) {
for my $k ( 1 .. $j ) {
my $p = Algorithm::Permute->new( [ $i, $j, $k ] );
while ( my @res = $p->next ) {
my $t = test_cardano(@res);
if ( $t == 1 ) {
push @triplets, \@res;
}
}
}
}
$i++;
last if $i > 1000;
}
for my $ct (@triplets) {
my ( $a, $b, $c ) = $ct->@*;
print <<"END";
A: $a\tB: $b\tC: $c
END
}
sub test_cardano ( $a, $b, $c ) {
my $sqrtc = sqrt $c;
# not necessary for the first five
if ( $a > $b * $sqrtc ) {
return cuberoot( $a + $b * $sqrtc ) + cuberoot( $a - $b * $sqrtc );
}
return cuberoot( $a + $b * $sqrtc ) +
-1 * cuberoot( abs( $a - $b * $sqrtc ) );
}
sub cuberoot ($n ) { return $n**( 1 / 3 ) }
A: 17 B: 18 C: 5
A: 17 B: 9 C: 20
A: 8 B: 3 C: 21
A: 11 B: 4 C: 29
A: 14 B: 5 C: 37