Fractions, Trees and Primes: Weekly Challenge 146
146 is octahedral.
TASK #1 › 10001st Prime Number
Submitted by: Mohammad S Anwar
Write a script to generate the 10001st prime number.
There may be more clever ways of finding the next one. A professor I had years ago is big on the hunt for higher and higher primes.
But, for this purpose, for this low a number, the brute force method of checking if each number is prime, and if so, iterating a counter, then ending when the count is up to 10001.
They’re not all jobs for recursion.
Show Me The Code!
#!/usr/bin/env perl
use strict;
use warnings;
use feature qw{ say postderef signatures state };
no warnings qw{ experimental };
my @primes;
my $c = 1;
my $n = 2;
while (1) {
if ( is_prime($n) ) {
if ( $c == 10001 ) {
say join "\t", $c, $n if $c == 10001;
exit;
}
$c++;
}
$n++;
}
sub is_prime ($n) {
for ( 2 .. sqrt $n ) { return unless $n % $_ }
return 1;
}
10001 104743
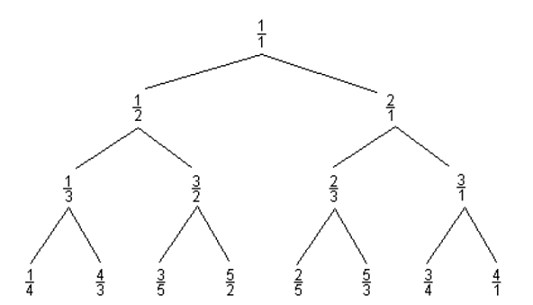
TASK #2 › Curious Fraction Tree
Submitted by: Mohammad S Anwar
Consider the following Curious Fraction Tree:
You are given a fraction, member of the tree created similar to the above sample.
Write a script to find out the parent and grandparent of the given member.
We’re given a tree, so I pulled out my old Node code to build the tree. I use the old-school OOP method because it’s portable.
Using Perl’s OOP, if the tree is correct, then each node will have a parent (which could be null), and each parent will have another parent (which could also be null), so we just have to check if $node->parent and $node->parent->parent are defined, and if so, get their value.
Kinda a softball for the first challenge of the year, I think.
I mean, thinking through to find a way to algorithmically create the graph, instead of building it by hand like I do, would be more interesting. The right of a given node is basically 1 + fraction: 1/1, 2/1, 3/1, 4,1, etc. With nodes with a left, it becomes harder but just as simple: 1/2 -> 3/2, 2/3 -> 5/3, etc.
The lefts are more complex. Starting with 1/1, we go to 1/2, 1/3, 1/4, and so on, but when there’s a right, like with 3/2, we go somewhere different, like 3/2. If it was just increment the denominator, you’d get 3/3, which simplifies to 1/1. One more and you get 3/4, but you get 3/4 from 3/1. Instead, it’s 3/5.
I’m sure that the left of 1/4 would be 1/5 and the right would be 5/4, but I’m not nearly as sure what the left and right of 4/3 would be.
Thankfully, that’s not the task.
Show Me The Code!
#!/usr/bin/env perl
use strict;
use warnings;
use feature qw{ say postderef signatures state };
no warnings qw{ experimental };
my %node;
for my $i (
qw{
1/1 1/2 2/1
1/3 3/2 2/3
3/1 1/4 4/3
3/5 5/2 2/5
5/3 3/4 4/1
}
)
{
$node{$i} = Node->new($i);
}
$node{'1/1'}->left( $node{'1/2'} ); # 1
$node{'1/1'}->right( $node{'2/1'} ); # 1
$node{'1/2'}->left( $node{'1/3'} ); # 2
$node{'1/2'}->right( $node{'3/2'} ); # 2
$node{'1/3'}->left( $node{'1/4'} ); # 3
$node{'1/3'}->right( $node{'4/3'} ); # 3
$node{'2/1'}->left( $node{'2/3'} ); # 2
$node{'2/1'}->right( $node{'3/1'} ); # 2
$node{'2/3'}->left( $node{'2/5'} ); # 3
$node{'2/3'}->right( $node{'5/3'} ); # 3
$node{'3/1'}->left( $node{'3/4'} ); # 3
$node{'3/1'}->right( $node{'4/1'} ); # 3
$node{'3/2'}->left( $node{'3/5'} ); # 3
$node{'3/2'}->right( $node{'5/2'} ); # 3
# maybe I should check to see if $node{$n}
# is defined as well. eh?
for my $n ( sort keys %node ) {
my $node = $node{$n};
my $parent = '';
my $grandparent = '';
if ( defined $node->parent ) {
$parent = $node->parent->value;
if ( defined $node->parent->parent ) {
$grandparent = $node->parent->parent->value;
}
}
say <<"END";
INPUT: \$member = "$n"
OUTPUT: parent = "$parent" and grandparent = "$grandparent"
END
}
package Node;
sub new ( $class, $value = 0 ) {
my $self = {};
$self->{value} = $value;
$self->{left} = undef;
$self->{right} = undef;
$self->{horizontal} = undef;
$self->{parent} = undef;
return bless $self, $class;
}
sub value ( $self, $value = undef ) {
if ( defined $value ) {
$self->{value} = $value;
}
else {
return $self->{value};
}
}
sub is_root ( $self ) {
return defined $self->{parent} ? 0 : 1;
}
sub is_leaf ( $self ) {
return ( !defined $self->{left} && !defined $self->{right} )
? 1
: 0;
}
sub left ( $self, $node = undef ) {
if ( defined $node ) {
$self->{left} = $node;
$node->{parent} = $self;
}
else {
return $self->{left};
}
}
sub right ( $self, $node = undef ) {
if ( defined $node ) {
$self->{right} = $node;
$node->{parent} = $self;
}
else {
return $self->{right};
}
}
sub horizontal ( $self, $node = undef ) {
if ( defined $node ) {
$self->{horizontal} = $node;
$node->{parent} = $self;
}
else {
return $self->{horizontal};
}
}
sub parent ($self ) {
return $self->{parent};
}
$ ./ch-2.pl
INPUT: $member = "1/1"
OUTPUT: parent = "" and grandparent = ""
INPUT: $member = "1/2"
OUTPUT: parent = "1/1" and grandparent = ""
INPUT: $member = "1/3"
OUTPUT: parent = "1/2" and grandparent = "1/1"
INPUT: $member = "1/4"
OUTPUT: parent = "1/3" and grandparent = "1/2"
INPUT: $member = "2/1"
OUTPUT: parent = "1/1" and grandparent = ""
INPUT: $member = "2/3"
OUTPUT: parent = "2/1" and grandparent = "1/1"
INPUT: $member = "2/5"
OUTPUT: parent = "2/3" and grandparent = "2/1"
INPUT: $member = "3/1"
OUTPUT: parent = "2/1" and grandparent = "1/1"
INPUT: $member = "3/2"
OUTPUT: parent = "1/2" and grandparent = "1/1"
INPUT: $member = "3/4"
OUTPUT: parent = "3/1" and grandparent = "2/1"
INPUT: $member = "3/5"
OUTPUT: parent = "3/2" and grandparent = "1/2"
INPUT: $member = "4/1"
OUTPUT: parent = "3/1" and grandparent = "2/1"
INPUT: $member = "4/3"
OUTPUT: parent = "1/3" and grandparent = "1/2"
INPUT: $member = "5/2"
OUTPUT: parent = "3/2" and grandparent = "1/2"
INPUT: $member = "5/3"
OUTPUT: parent = "2/3" and grandparent = "2/1"