Ugly and Square: Perl Weekly Challenge #123
TASK #1 › Ugly Numbers
Submitted by: Mohammad S Anwar
You are given an integer $n >= 1.Write a script to find the $nth element of Ugly Numbers.
Ugly numbers are those number whose prime factors are 2, 3 or 5. For example, the first 10 Ugly Numbers are 1, 2, 3, 4, 5, 6, 8, 9, 10, 12.
ETA: I got this wrong. Corrected in another blog post.
I thought about Recursion, because I know my brand, but really, no. This is perfectly doable in an iterative way. I do it with an infinite while, but I could’ve done for ( my $i = 1; $i <= $n ; ) { ... } and iterate within the loop only when we find another Ugly Number, or something like that.
Show Me The Code
#!/usr/bin/env perl
use feature qw{say state signatures};
use strict;
use warnings;
use utf8;
no warnings qw{ experimental };
use Carp;
use Getopt::Long;
my $n = 8;
GetOptions( 'n=i' => \$n, );
carp 'Bad Input' unless $n > 0;
my $u = get_ugly($n);
say "Input: \$n = $n";
say "Output: $u";
sub get_ugly ( $n ) {
return 1 if $n == 1;
my $c = 1;
my $u = 0;
while (1) {
$u++;
my $f = 0;
$f = 1 if $u % 2 == 0;
$f = 1 if $u % 3 == 0;
$f = 1 if $u % 5 == 0;
$c++ if $f;
return $u if $n == $c;
}
}
$ time ./ch-1.pl -n 2000067
Input: $n = 2000067
Output: 2727363
real 0m0.645s
user 0m0.563s
sys 0m0.047s
$ time ./ch-1.pl -n 20000678
Input: $n = 20000678
Output: 27273651
real 0m6.482s
user 0m6.328s
sys 0m0.016s
$ time ./ch-1.pl -n 200006789
Input: $n = 200006789
Output: 272736530
real 1m11.287s
user 1m9.078s
sys 0m0.297s
TASK #2 › Square Points
Submitted by: Mohammad S Anwar
You are given coordinates of four points i.e. (x1, y1), (x2, y2), (x3, y3) and (x4, y4).Write a script to find out if the given four points form a square.
How are squares defined? Four sides of equal length and four corners with equal angles. If it has equal angles but not equal sides, it’s a rectangle. If it has equal sides but not equal angles, it’s a parallelogram. So, given points A, B, C, and D, you need to compare the distances A->B, B->C, C->D and D->A. But you also need to check the angles ABC, BCD, CDA and DAC.
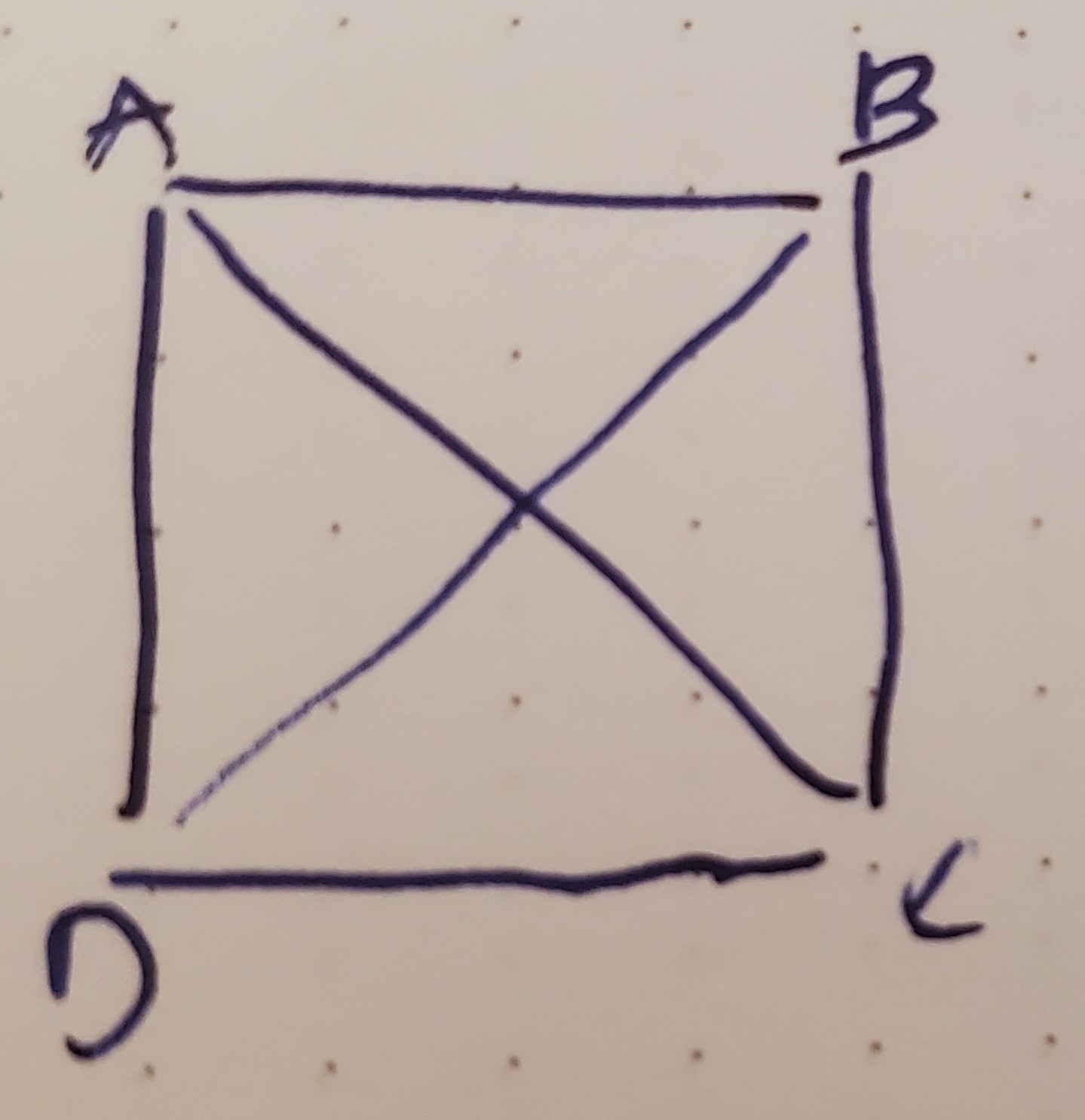
Or do you?
Because if ABCD is a parallelogram, A->C will be wildly different from B->D, while for a square, they will be equal.
Plus, you only have to remember one formula from high school math, c2 = a2 + b2, which we change to c = √a2 + b2, or c = √ (abs(x1 - x2 ))2 + (abs(y1 - y2 ))2
(I first wrote it with abs, but since a negative number multiplied by a negative number is a positive number, this should be unnecessary. Ah well. I do have some belt-and-suspenders tendencies…)
Speaking of, I wrote a graphing function to show me the whole, but removed it, because I was starting to think through parallelograms and it wouldn’t have handled floating-point locations. Maybe a HTML/JS/CSS/SVG version would be the way to show the points and shape, as well as discerning if it’s square or not. Looks like I’ll want to make a second solution and blog post.
Show Me The Code
#!/usr/bin/env perl
use feature qw{say state signatures};
use strict;
use warnings;
use utf8;
no warnings qw{ experimental };
use JSON;
my $json = JSON->new->canonical;
my @data = (
[ [ 10, 20 ], [ 20, 20 ], [ 20, 10 ], [ 10, 10 ], ],
[ [ 12, 24 ], [ 16, 10 ], [ 20, 12 ], [ 18, 16 ], ],
[ [ 40, 40 ], [ 50, 30 ], [ 40, 20 ], [ 30, 30 ], ],
[ [ 10, 10 ], [ 15, 15 ], [ 20, 15 ], [ 15, 10 ], ],
);
for my $d (@data) {
say $json->encode($d);
say is_square($d);
say '';
}
sub is_square($d) {
my @objs = $d->@*;
my @distances;
push @distances, distance( @objs[ 0, 1 ] ); # A -> B
push @distances, distance( @objs[ 1, 2 ] ); # B -> C
push @distances, distance( @objs[ 2, 3 ] ); # C -> D
push @distances, distance( @objs[ 3, 0 ] ); # D -> A
push @distances, distance( @objs[ 0, 2 ] ); # A -> C
push @distances, distance( @objs[ 1, 3 ] ); # B -> D
# sides are of equal length
return 0 if $distances[0] != $distances[1];
return 0 if $distances[1] != $distances[2];
return 0 if $distances[2] != $distances[3];
return 0 if $distances[3] != $distances[0];
# distances throught the center are of equal length
# removing parallelograms
return 0 if $distances[4] != $distances[5];
return 1;
}
sub distance ( $p1, $p2 ) {
return
sqrt( ( ( $p1->[0] - $p2->[0] )**2 ) +
( ( $p1->[1] - $p2->[1] )**2 ) );
}
[[10,20],[20,20],[20,10],[10,10]]
1
[[12,24],[16,10],[20,12],[18,16]]
0
[[40,40],[50,30],[40,20],[30,30]]
1
[[10,10],[15,15],[20,15],[15,10]]
0