Thoughts on an If/Else: Perl Challenge 87
First, we consider the challenge.
TASK #1 › Longest Consecutive Sequence
Submitted by: Mohammad S Anwar
You are given an unsorted array of integers @N.Write a script to find the longest consecutive sequence. Print 0 if none sequence found.
First, let us note words that are not in this challenge. Positive and unique stand out to me. Non-zero is also absent. This will have to accept -1, -1, 0, -1 as an acceptable input, even if the examples all use unique, positive, non-zero integers.
My take on this is to first sort the unsorted array, then create an array of arrays, each sub-array being a sequence.
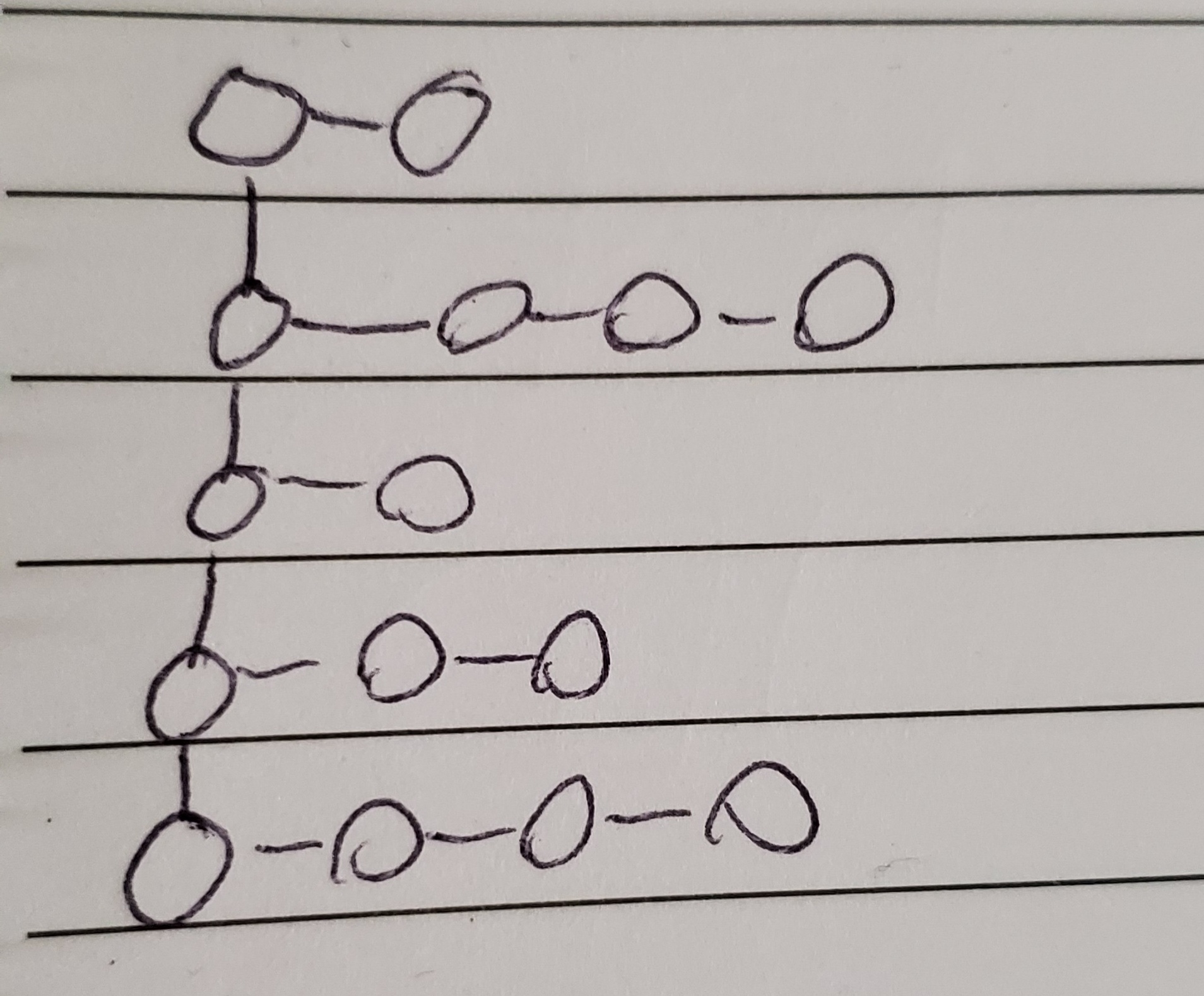
Taking the array -1, -1, 0, -1, 7, 13, 15 as an example, the multidimensional array would look like:
[[-1, 0], [7], [13, 15]];
But that isn’t the most helpful. We can then sort by sequence length to ensure that the longest ones are first.
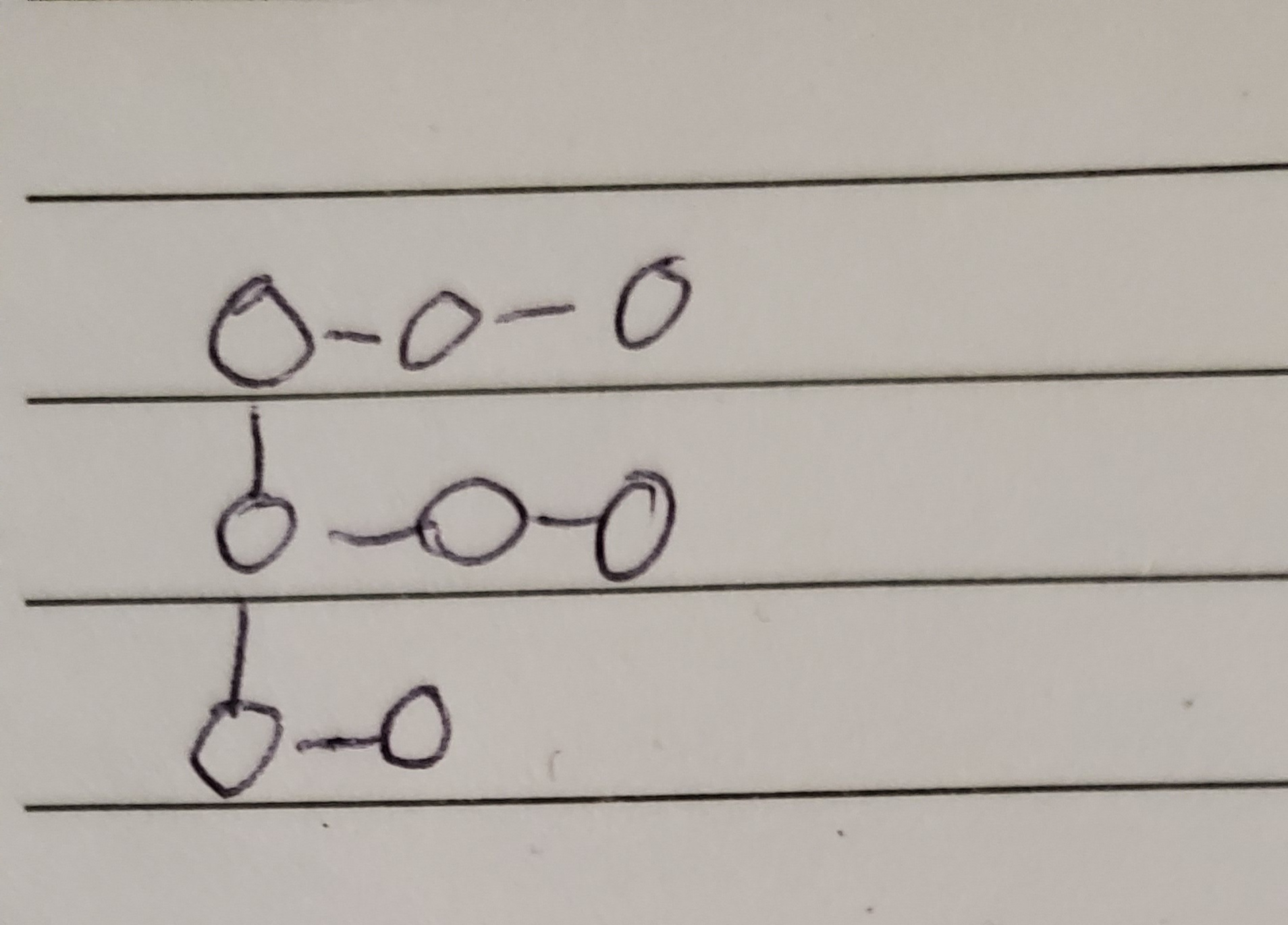
[[-1, 0], [13, 15], [7]];
We then take the first and go from there.
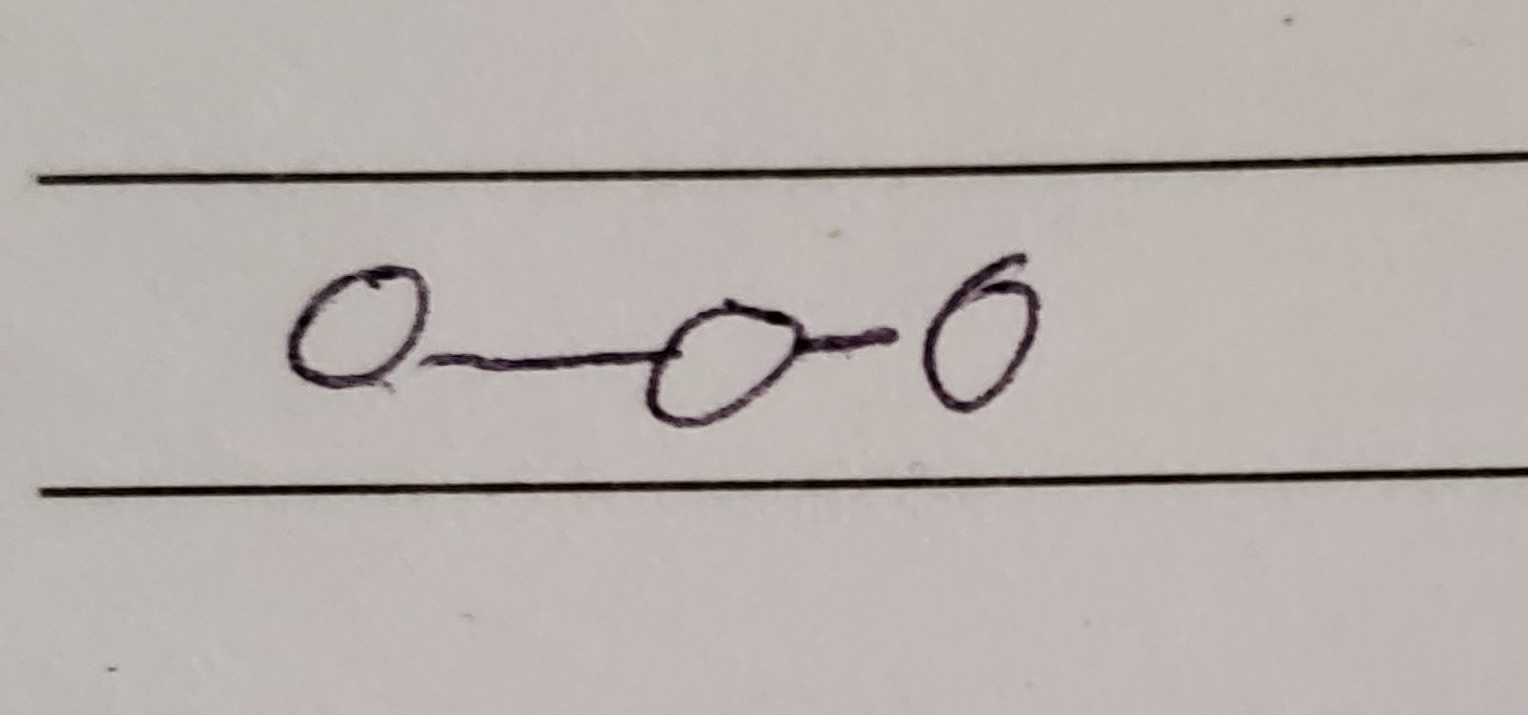
[-1, 0]
Aside
Looking back, I’m struck that having two arrays, current and longest, and copying current onto longest when current is as long or longer than longest. It’s a good implementation, but it is not what I wrote.
What I wrote
I use subroutine signatures. Your syntax may vary.
my $zed = [];
my $n = 0;
for my $i ( uniq sort { $a <=> $b } @array ) {
if ( !$zed->[$n][-1] || $i == $zed->[$n][-1] + 1 ) {
# this is intentionally empty
}
else {
$n++;
}
push $zed->[$n]->@*, $i;
}
Two words: sorted and unique. Sorting makes the process easier, because then you only have to compare the current integer with the previous integer, instead of the whole array. And uniqueness removes a hinderance, because with 1, 2, 2, 3, the second 2 is not 2 + 1, so you might end up with 1, 2 as your longest sequence if you’re not careful. Thus uniq sort { $a <=> $b }.
(By default, Perl sorts alphabetically, which gives the order 69,7,70 instead of 7,69,70. Perl things more in terms of text than numbers, which is fine but important to remember.)
Which gets to the reason I decided to blog this.
if ( !$zed->[$n][-1] || $i == $zed->[$n][-1] + 1 ) {
# this is intentionally empty
}
else {
$n++;
}
In long form: if there’s nothing in the current sequence, or if the current integer is the integer following the last integer in the current sequence, do nothing. Otherwise, increment the sequence index.
Or as I wrote on Twitter the other day,
if ( conditions ) { }
else { $n++ }
This works. It is clear. It contains a no-op block. I hate it, but I hate it not quite enough to rewrite it.
I mean, the logic is clear to me, and changing it to negate it all is likely going to be pretzel logic, or instead:
if ( !( conditions ) ) { $n++ }
Which looks to me like a code version of this My Cousin Vinny line:

Sawyer X suggests
conditions or $n++ ;
That’s nice. I like that. I’m going with it.